Ante Qu
I graduated as of June 2021 with a PhD in Computer Science from Stanford University, where I was advised by Doug L. James and was supported by a NSF Graduate Research Fellowship.
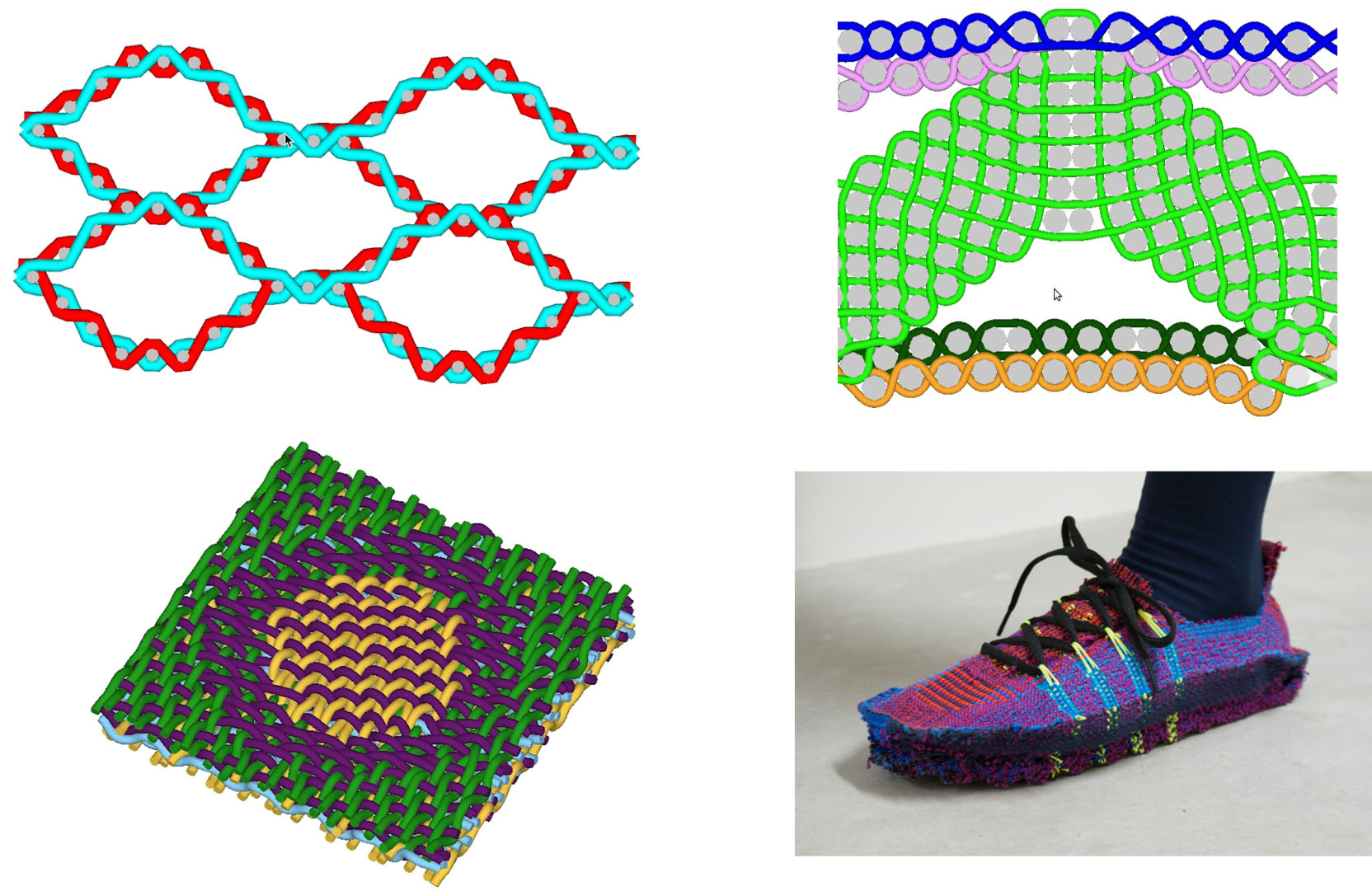
My primary research interests are in physics simulations for computer graphics. I develop topology certificates for yarn-level clothing animations, and I used to numerically simulate sound for computer animations.
I was formerly a full-time software engineer at Microsoft, where I worked on the Office Graphics (PowerPoint, Word, Excel) team. I graduated in 2015 with an AB in Physics from Princeton University, where I was advised by Jason Fleischer. I have also worked on research projects at Columbia University, the Princeton Plasma Physics Lab, Adobe Research, and the Toyota Research Institute.
Outside of work, I also enjoy board games, bridge, hiking, Star Trek, and food.
Research
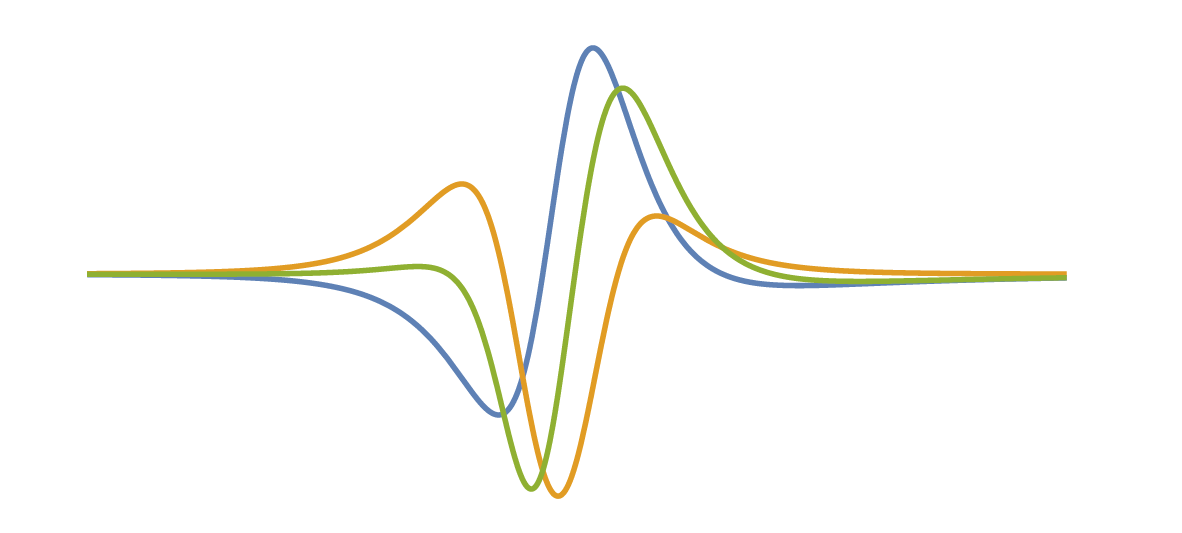
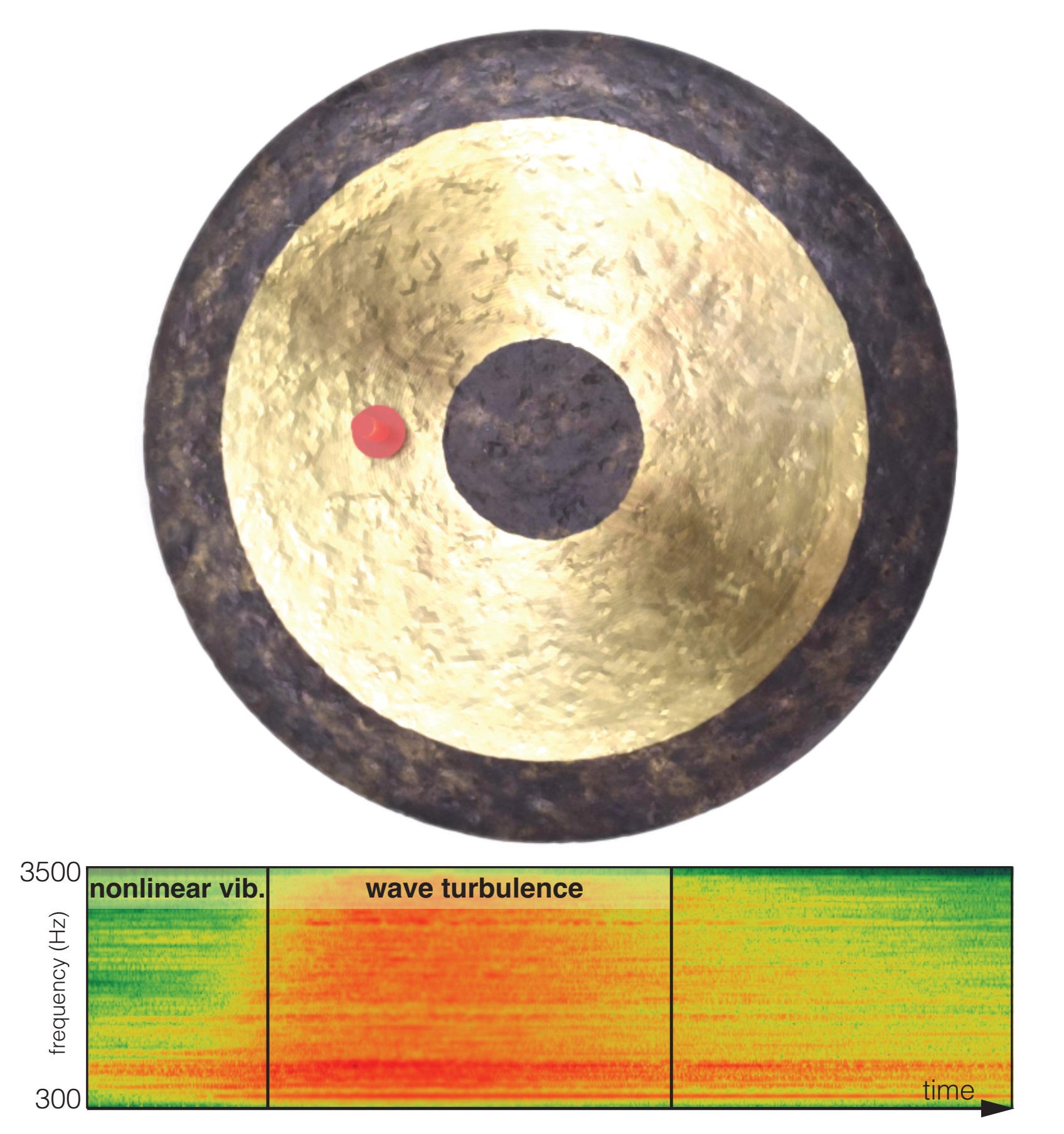
We propose a physically based, multi-scale reduced simulation method to synthesize nonlinear thin-shell sounds. We first split nonlinear vibrations into two scales, with a small low-frequency part simulated in a fully nonlinear way, and a high-frequency part containing many more modes approximated through time-varying linearization. This allows us to capture interesting nonlinearities in the shells’ deformation, tens of times faster than previous approaches. Furthermore, we propose a method that enriches simulated sounds with wave turbulent sound details through a phenomenological diffusion model in the frequency domain, and thereby sidestep the expensive simulation of chaotic high-frequency dynamics. We show several examples of our simulations, illustrating the efficiency and realism of our model.
Our algorithm performs a decomposition of the image into basis functions and searches for the coefficients that yield the flattest output intensity pattern. This algorithm takes advantage of the fact that a relatively small number of basis elements can store the majority of the information in the image. Popular phase retrieval methods such as the Gerchberg–Saxton algorithm can only converge to the phase image under light that is sufficiently coherent. From our simulations, we find that our method consistently produces correlations of over 99% with the original phase image, using either incoherent or coherent light and only 10% as many basis elements as the number of pixels in the image. We believe this result is a strong indication that this method will be able to reliably retrieve a direct phase image in the laboratory.
Teaching
- Stanford University — CS 205A: Mathematical Methods for Robotics, Vision, and Graphics, Winter 2018 Course Assistant
- Stanford University — CS 348C: Computer Graphics: Animation and Simulation, Fall 2017 Course Assistant
- Princeton University — PHY 104: General Physics II, Spring 2014 Grader
- Princeton University — MAT 321: Numerical Methods, Spring 2014 Grader
Service
- 2021, ACM Siggraph Asia, Reviewer
- 2020, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2020), Reviewer
- 2020, Eurographics & Eurovis (EGEV 2020), Reviewer